Pernahkah
kalian mendengar tentang dalil l’Hospital? Ya dalil ini berkaitan erat dengan topik matematika
tentang limit. Dalil tersebut banyak dikenalkan oleh kalangan pengajar pada
siswa sebagai suatu ‘cara cepat’ atau ‘cara mudah’ untuk menghitung nilai limit
suatu fungsi. Walaupun pada prakteknya tetap saja ada banyak fungsi yang susa
dicari nilai limitnya meski sudah menggunakan dalil atau metode l’Hospital.
Seperti apakah dalil l’Hospital itu? Mari kita pelajari!
Untuk menghitung nilai limit suatu fungsi f(x) dimana x
mendekati a, kita bisa menghitungnya dengan mensubstitusikan nilai x = a pada
fungsi f(x) tersebut. Akan tetapi setelah disubstitusikan nilai x = a, beberapa
fungsi justru menunjukkan hasil 0/0 yang artinya nilai limit fungsi tersebut tidak
dapat diketahui. Padahal, terkadang sebenarnya grafik f(x) pada
posisi x = a memiliki nilai limit yang jelas. Oleh karena itu, diperlukan
metode lain yang dapat digunakan untuk menghitung nilai limit fungsi tersebut. Pada
dasarnya ada banyak metode yang dapat digunakan untuk menghitung nilai limit
fungsi pada kasus di atas. Beberapa
metode tersebut adalah metode pemfaktoran dan metode perkalian sekawan yang
dapat dipelajari pada artikel sebelumnya (Klik disini). Namun, banyak siswa yang
kurang bisa memahami proses yang panjang dari metode tersebut walaupun sebenarnya
metode tersebut baik dan bagus untuk dipahami dan dipelajari sebagai dasar
untuk mempelajari kalkulus. Sebagai solusi banyak yang kemudia
beralih menggunakan metode I’Hospital. Bagaimana cara penggunaan metode
tersebut? Lihat contoh berikut.
Dalil I’Hospital
Carilah
nilai limit dari fungsi berikut!
Langkah-langkah menghitung nilai limit fungsi diatas menggunakan dalil I’Hospital
yaitu sebagai berikut:
1.
Pastikan
bahwa fungsi tersebut tidak dapat dicari nilai limitnya dengan metode
substitusi karena hasilya 0/0.
2. Carilah hasil turunan
pertama pembilang dan turunan pertama penyebut. Nilai limit dari fungsi di atas
adalah sama dengan limit fungsi hasil turunan tersebut.
Sehingga,
3.
Substitusikan nilai x = a pada fungsi yang
baru. Jika hasil substitusi terdefinisi (tidak 0/0 lagi) maka hasil tersebut
merupakan nilai limit dari fungsi di atas. Jika hasil substitusi masih
menunjukkan 0/0 maka kembali ke langkah 2 dimana fungsi yang baru kembali
didifferensialkan satu tingkat (turunan kedua pembilang dan penyebut di atas) kemudian
disubstitusikan. Langkah ini terus berlanjut sampai hasil substitusi
terdefinisi.
Jadi nilai limit fungsi
di atas pada x mendekati -1 adalah 1.
Apakah
kalian paham dengan dalil I’Hospital di atas? Mari kita lihat contoh lain yang sedikit
lebih sulit dan kompleks. Perlu diingat bahwa tidak semua fungsi menjadi lebih
mudah dengan metode I’Hospital. Nanti akan kita lihat contohnya.
Contoh Soal:
Carilah
nilai limit fungsi berikut!
Jawab:
a.
Kita coba dengan metode substitusi
Karena hasil substitusi menujukkan 0/0
maka dalil I’Hospita bisa digunakan. Kita
ubah pembilang dan penyebut dari fungsi di atas menjadi turunan pertamanya.
Kemudian kita substitusikan kembali x = 0.
Karena hasilya masih 0/0 maka kita
lanjutkan dengan mencari turunan kedua dari fungsi diatas. Kemudia
substitusikan kembali x = 0
Karena hasilnya masih 0/0 maka kita ubah
fungsi tersebut menjadi turunan ketiganya. Kemudian coba substitusikan kembali
nilai x = 0.
Jadi nilai limit diatas
adalah
b.
Sama dengan langkah di atas, pertama kita coba
substitusikan nilai x = 0
Karena hasilnya 0/0 maka pembilang
dan penyebut fungsi diubah menjadi turunan pertamanya. Kemudian kita coba lagi
substitusikan x = 0.
Jadi nilai limit fungsi di atas adalah
Demikian artikel
tentang Dalil I’Hospital. Jika ada pertanyaan silahkan tuliskan pada kolom
komentar.













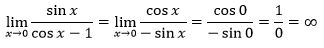








No comments:
Post a Comment
Penulis mengharapkan komentar, kritik, dan saran agar blog ini semakin baik kedepannya :)