Limit merupakan salah satu topik matematika yang mulai
dipelajari pada jenjang SMA kelas XI. Topik ini sangatlah penting karena menjadi dasar bagi
mereka yang ingin belajar tentang kalkulus. Pada artikel kali ini, saya tidak
akan membahas tentang definisi atau konsep dasar dari limit itu sendiri
melainkan cara mencari atau menentukan nilai limit suatu fungsi dengan berbagai
metode. Seperti yang sudah kita tahu, ada banyak cara atau metode untuk mencari
nilai limit suatu fungsi tergantung dari karakteristik fungsi ang akan dicari
nilai limitnya. Oke, langsung saja mari kita pelajari!
Metode Substitusi
Pada dasarnya untuk mencari nilai limit suatu fungsi
misalnya untuk x mendekati a maka nilai limit fungsi tersebut dapat
diperoleh dengan cara men-substitusi-kan nilai x = a pada fungsi tersebut. Contoh
penggunaan metode substitusi yaitu sebagai berikut:
Contoh Soal 1:
Carilah nilai limit
fungsi berikut!
Jawab:
Sekarang lihatlah contoh limit berikut:
Jika kita cari limitnya dengan metode substitusi maka kita akan memperoleh hasil:
Padahal apabila kita
lihat grafik dari fungsi tersebut maka nilai limit pada x = -1 adalah 1. Untuk
kasus fungsi yang seperti contoh di atas dimana setelah disubstitusikan nilai x
= a hasilnya menunjukkan kondisi 0/0 maka metode susbtitusi tidak dapat
digunakan. Sebagai gantinya, untuk mencari nilai limit fungsi seperti di atas
harus digunakan metode lain seperti metode-metode berikut.
Metode Pemfaktoran
Metode pemfaktoran pada dasarnya sama dengan metode
substitusi yaitu dengan mensubstitusikan nilai x = a ke dalam fungsi yang akan
dicari nilai limitnya. Bedanya, sebelum mensubstitusikan nilai x = a, fungsi
harus terlebih dahulu disederhanakan dengan cara menghilangkan faktor penyebab
nilai fungsi menjadi 0/0. Hal ini dapat dilakukan dengan cara memfaktorkan
masing-masing pembilang dan penyebut fungsi. Contoh penggunaan metode ini yaitu
sebagai berikut:
Contoh Soal 2:
Carilah nilai limit fungsi berikut!
Jawab:
a.
Pertama faktorkan
bagian pembilang dan penyebut fungsi. Kemudian sederhanakan dengan
menghilangkan faktor yang sama (Faktor penyebab nilai fungsi 0/0).
Setelah disederhanakan,
nilai limit bisa cari dengan cara mensubtitusikan nilai x = 2.
b.
Pertama faktorkan bagian pembilang dan penyebut fungsi,
kemudian sederhanakan. Fungsi pada soal di
atas merupakan bentuk a2 – b2 = (a + b)(a - b) sehingga
c.
Pertama faktorkan bagian pembilang dan penyebut fungsi,
kemudian sederhanakan. Fungsi pada soal di
atas dapat difaktorkan dengan metode pemfaktoran Horner. Sehingga diperoleh
hasil yaitu:
Jadi nilai limitnya adalah
Sekarang lihat contoh soal lain
berikut ini:
Semua nilai limit di atas apabila kita substitusikan
nilai x = a maka hasilnya menunjukkan kondisi 0/0. Ini berarti metode
substitusi tidak dapat digunakan untuk mencari nilai limit diatas. Lalu apakah
metode pemfaktoran bisa digunakan? Jika kita lihat bentuk fungsi pada limit di
atas rasanya mustahil untuk kita memfaktorkan dan menghilangkan faktor pembuat
fungsi menjadi 0/0. Lalu metode apa yang bisa digunakan untuk mencari limit di
atas? Mari kita pelajari metode yang lain!
Metode Mengalikan dengan Faktor Sekawan (conjugate)
Selain metode pemfaktoran di atas,
ada pula metode lain untuk mencari nilai limit suatu fungsi yaitu metode
mengalikan dengan faktor sekawan dari pembilang dan penyebut fungsi yang akan
di cari limitnya. Hal ini bertujuan agar fungsi tersebut dapat difaktorkan dan
disederhanakan sehingga bisa dicari nilai limitnya dengan metode substistusi. Mari kita lihat contoh penggunaan metode ini pada contoh
soal di atas.
Contoh Soal 3:
Jawab:
a. Pertama, kalikan penyebut fungsi dengan faktor
sekawannya. Pembilang tidak perlu dikalikan dengan faktor sekawannya karena
tidak dalam bentuk akar sehingga mudah saja nantinya untuk
difaktorkan/disederhanakan.
Setelah dikalikan, sederha fungsi tersebut dengan cara
memfaktorkannya dan menghilangkan faktor yang sama.
Cari
nilai limitnya dengan cara mensubstitusikan nilai x = 1
Jadi
nilai liminya adalah
b. Pertama, kalikan
penyebut dan pembilang fungsi dengan faktor sekawannya masing-masing. Bagian yang
berwarna biru merupakan sekawan dari penyebut dan bagian yang berwarna merah
merupakan sekawan dari pembilang.
Sederhanakan hasil perkalian
tersebut.
Sehingga,
Dengan metode substitusi maka kita
dapat mencari nilai limitnya yaitu:
Ada satu metode lain untuk mencari nilai
limit fungsi yang nilainya 0/0 apabila di substitusikan nilai x = a. Metode
tersebut adalah metode L’Hospital. Penggunaan metode ini akan dibahas pada
artikel selnajutnya. Jika ada pertanyaan silahkan tulis pada kolom komentar.













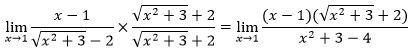














Min... Contoh 3 yang a itu salah jawabannya... Mohon di cek kembali... Terima kasih
ReplyDeleteJawabannya benar, tapi soal nya saja saya yang salah ketik. harusnya yang dibawah akar itu (x^2 + 3x). Thanks koreksinya :)
DeleteMetode substitusi sama pemfaktoran pada dasarnya sama atau beda ya?
ReplyDeleteKalo yg tak terhingga gmna min?
ReplyDeleteIn this fashion my partner Wesley Virgin's report starts with this shocking and controversial VIDEO.
ReplyDeleteWesley was in the army-and soon after leaving-he revealed hidden, "self mind control" secrets that the CIA and others used to get everything they want.
THESE are the EXACT same methods many famous people (notably those who "became famous out of nothing") and top business people used to become rich and successful.
You've heard that you only use 10% of your brain.
Really, that's because most of your brainpower is UNTAPPED.
Maybe this conversation has even occurred INSIDE OF YOUR own head... as it did in my good friend Wesley Virgin's head around seven years back, while driving an unregistered, trash bucket of a car with a suspended driver's license and $3.20 on his debit card.
"I'm absolutely fed up with living paycheck to paycheck! Why can't I turn myself successful?"
You've taken part in those types of conversations, right?
Your success story is going to happen. All you need is to believe in YOURSELF.
CLICK HERE TO LEARN WESLEY'S SECRETS