Sistem persamaan linear dua variabel adalah salah satu
topik yang dibahas pada jenjang SMP kelas VIII. Topik ini berkaitan erat dengan
topik sistem persamaan linear satu variabel (SPLSV) dan garis lurus. Berikut ini
akan dibahas beberapa contoh masalah SPLDV dan berbagai metode untuk
menyelesaikan atau menjawabnya.
Contoh Masalah:
Suatu ketika Toni membeli satu tas dan dua pasang sepatu
di salah satu toko di Surabaya. Toni harus membayar total Rp210.000,00. Dilain
waktu, Silva membeli tiga tas dan satu pasang sepatu dengan merek yang sama dan
di toko yang sama seharga total Rp390.000,00. Berapakah masing-masing harga tas
dan sepatu tersebut?
Jawab:
Untuk menyelesaikan masalah SPLDV yang disajikan dalam
bentuk soal cerita, kalian perlu mengubah terlebih dahulu soal cerita di atas
ke dalam bahasa matematika.
Misalkan Harga
satu tas adalah T dan Harga satu
pasang sepatu adalah S maka:
- Toni à 1 Tas dan 2 sepatu total Rp210.000,00 à T + 2S = 210
- Silva à 3 Tas dan 1 sepatu total Rp390.000,00 à 3T + S = 390
Harga di atas disederhanakan menjadi dengan cara dibagi
1000 agar lebih mudah. Jika nilai T dan S telah ditemukan maka nilainya harus dikalikan kembali
dengan 1000. Setelah soal cerita di atas diubah ke dalam bahasa matematika,
maka kita bisa menyelesaikannya dengan salah satu metode berikut:
Cara 1: Metode Grafik
Permasalahan SPLDV di atas dapat diselesaikan
dengan metode grafik yaitu dengan menggambar grafik dari masing-masing persamaan
dan menemukan titik potongnya. Untuk mesalah di atas maka:
Dengan demikian grafiknya akan menjadi:
Jadi, Harga satu tas yang dibeli Toni dan Silva adalah
Rp114.000,00. Sedangkan, harga sepatu yang mereka beli adalah Rp48.000,00.
Seperti yang kita lihat di atas, metode grafik cukup sulit
digunakan jika koordinate titik mencapai puluhan bahkan ratusan atau ribuan. Metode
grafik cukup merepotkan juga karena harus menggambar grafik terlebih dahulu dan
terkadang titik penyelesaian tidak selalu berapa pada posisi yang mudah
diketahui nilainya.
Cara 2: Metode Substitusi
Metode yang kedua yaitu metode substitusi. Metode ini tidak memerlukan siswa untuk
menggambar grafik. Misal dari contoh masalah diatas, setelah masalah diubah ke
dalam kalimat matematika maka langkah selanjutnya adalah:
Variable T pada persamaan (3) disubstitusikan
ke persamaan (2)
Nilai S telah ditemukan, untuk mencari
nilai T maka substitusikan nilai s pada pers (4) ke pers (3). Sehingga
diperoleh,
Jadi, diperoleh bahwa
Metode substitusi lebih mudah digunakan dibanding
metode grafik jika soal tersebut melibatkan angka yang cukup besar. Namun,
metode ini cukup melibatkan persamaan tambahan.
Cara 3: Metode Eliminasi
Metode eliminasi tidak memerlukan gambar grafik
dan hanya berkutat dengan persamaannya saja sama seperti metode substitusi.
Setelah mengubah masalah ke dalam kalimat matematika, maka langkah yang perlu
dilakukan yaitu:
Misalkan variabel S akan kita eliminasi,
maka koefisien S pada kedua persamaan harus disamakan terlebih dahulu. Cara
mudah menyamakan koefisiennya adalah dengan mengalikan pers 1 dengan koefisien
S pada pers 2 dan sebaliknya.
Setelah koefisien sama maka dilakukan
eliminasi.
Untuk mencari nilai S maka dilakukan
eliminasi pada T. Untuk itu kita kembali lagi pada pers (1) dan (2) kemudian menyamakan
koefisien T karena T akan dieliminasi.
Jadi diperoleh nilai T=114 dan S=48. Dengan demikian harga satu tas adalah Rp114.000,00 dan harga
satu pasang sepatu adalah Rp48.000,00.
Metode eliminasi cukup mudah digunakan, tetapi cukup panjang karena
ada dua kali proses eliminasi.
Cara 4: Metode Eliminasi dan Substitusi
Metode ini sebenarnya gabungan dari metode
eliminasi dan metode substitusi di atas. Pada
langkah awal metode ini digunakan cara eliminasi untuk mencari nilai salah satu
variabel. Kemudian, untuk mencari nilai variabel kedua digunakan metode
substitusi dengan cara mensubstitusikan nilai yang diperoleh pada proses
eliminasi kedalam salah satu pers yang diberikan. Contoh:
Misalkan variabel S akan kita eliminasi,
maka koefisien S pada kedua persamaan harus disamakan terlebih dahulu kemudian
dieliminasi.
Kemudian, untuk mencari nilai S, nilai T tersebut disubstitusikan
pada salah satu persamaan T + 2S = 210 atau
3T + S = 390.
Jadi nilai S adalah 48. Dengan demikian, harga satu tas adalah Rp114.000,00
dan harga sepasang sepatu adalah Rp48.000,00
Metode eliminasi dan substitusi ini sering pula disebut sebagai
metode campuran untuk menyelesaikan masalah SPLDV. Metode campuran ini yang
paling banyak digunakan oleh para matematikawan untuk menyelesaikan
permasalahan SPLDV. Sebenarnya
ada satu lagi metode yang melibatkan penggunaan matrix. Metode ini akan dibahas
pada artikel lain secara terpisah.
Sekian artikel tentang menyelesaikan SPLDV.
Jika ada pertanyaan silahkan tulis di kolom kometar. Terima kasih











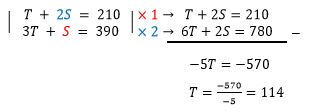








No comments:
Post a Comment
Penulis mengharapkan komentar, kritik, dan saran agar blog ini semakin baik kedepannya :)